Spray

Spray Equations

This section outlines the modeling and mathematics for the spray routines. Firstly, spray modeling relies on the following assumptions:

• Dilute spray: droplet volume inside an Eulerian cell is much smaller than the volume of the gas phase; the droplets can be modeled as Lagrangian point source terms relative to the Eulerian gas phase

• Infinite conductivity model: temperature within a droplet is temporally varying but spatially uniform

• One-third rule: the thermophysical properties in the film of an evaporating droplet can be approximated as a weighted average of the state at the droplet surface (weighted as 2/3) and the state of the surrounding gas (weighted as 1/3)

• Ideal equilibrium: the liquid and vapor state at the surface of the droplet are in equilibrium

• The radiation, Soret, and Dufour effects are neglected

Secondly, accurate spray modeling depends on accurate thermophysical and transport properties for both the gas and liquid phases. Gas-phase properties are obtained directly from the mechanism files in PelePhysics, while liquid-phase properties are derived from user-provided inputs for each liquid fuel species. Currently, two approaches are available for estimating liquid fuel properties:

• The original PeleMP [1] method, which utilizes a combination of constant values and temperature-based fits.

• A group contribution method (GCM) based on the work of Constantinou & Gani [2] [3] and Govindaraju & Ihme [4], previously implemented and validated in FuelLib.

Further details on the required inputs, as well as the formulations of both component-level and mixture-level liquid-phase properties, are provided in the Liquid Spray Properties section.

The evaporation models follow the work by Abramzon and Sirignano [5] and the multicomponent evaporation is based on work by Tonini. [6] Details regarding the energy balance are provided in Ge et al. [7] The subscript notation for this section is: \(d\) relates to the liquid droplet, \(v\) relates to the vapor state that is in equilibrium with the liquid and gas phase, \(L\) relates to the liquid phase, and \(g\) relates to the gas phase. The subscript \(r\) relates to the reference state with which to approximate the thermophysical and transport properties. This reference state is assumed to be in the evaporating film that surrounds the droplet state and is approximated as

\[ \begin{align}\begin{aligned}T_r &= T_d + A (T_g - T_d)\\Y_{r,n} &= Y_{v,n} + A (Y_{g,n} - Y_{v,n})\end{aligned}\end{align} \]

where \(A = 1/3\) according the the one-third rule. Additional nomenclature: \(M_n\) is the molar mass of species \(n\), \(\overline{M}\) is the average molar mass of a mixture, \(\mathcal{R}\) is the universal gas constant, \(N_L\) is the number of liquid species, and \(N_s\) is the number of gas phase species. \(Y_n\) and \(\chi_n\) are the mass and molar fractions of species \(n\), respectively. The user is required to provide a reference temperature for the liquid properties, \(T^*\), the critical temperature for each liquid species, \(T_{c,n}\), the boiling temperature for each liquid species at atmospheric pressure, \(T^*_{b,n}\), the latent heat and liquid specific heat at the reference temperature, \(h_{L,n}(T^*)\) and \(c_{p,L,n}(T^*)\), respectively. Note: this reference temperature is a constant value for all species and is not related to the reference state denoted by the subscript \(r\).

The equations of motion, mass, momentum, and energy for the Lagrangian spray droplet are:

\[ \begin{align}\begin{aligned}\frac{d \mathbf{X}_d}{d t} &= \mathbf{u}_d,\\\frac{d m_d}{d t} &= \sum^{N_L}_{n=0} \dot{m}_n,\\m_d \frac{d Y_{d,n}}{d t} &= \dot{m}_n - Y_{d,n} \frac{d m_d}{d t},\\m_d \frac{d \mathbf{u}_d}{d t} &= \mathbf{F}_d + m_d \mathbf{g},\\m_d c_{p,L} \frac{d T_d}{d t} &= \sum^{N_L}_{n=0} \dot{m}_n h_{L,n}(T_d) + \mathcal{Q}_d.\end{aligned}\end{align} \]

where \(\mathbf{X}_d\) is the spatial vector, \(\mathbf{u}_d\) is the velocity vector, \(T_d\) is the droplet temperature, \(m_d\) is the mass of the droplet, \(\mathbf{g}\) is an external body force (like gravity), \(\dot{m}\) is evaporated mass, \(\mathcal{Q}_d\) is the heat transfer between the droplet and the surrounding gas, and \(\mathbf{F}_d\) is the momentum source term. The density of the liquid mixture, \(\rho_d\), depends on the liquid mass fractions of the dropet, \(Y_{d,n}\),

\[\rho_d = \left( \sum^{N_L}_{n=0} \frac{Y_{d,n}}{\rho_{L,n}} \right)^{-1}\]

The droplets are assumed to be spherical with diameter \(d_d\). Therefore, the mass is computed as

\[m_d = \frac{\pi}{6} \rho_d d_d^3\]

The procedure is as follows for updating the spray droplet:

1. Interpolate the gas phase state to the droplet location using a trilinear interpolation scheme.

2. Compute the boiling temperature for species \(n\) at the current gas phase pressure using the Clasius-Clapeyron relation

   \[T_{b,n} = \left(\log\left(\frac{p_{\rm{atm}}}{p_g}\right) \frac{\mathcal{R}}{M_n h_{L,n}(T^*_{b,n})} + \frac{1}{T^*_{b,n}}\right)\]

   The boiling temperature of the droplet is computed as

   \[T_{d,b} = \sum^{N_L}_{n=0} Y_{d,n} T_{b,n}\]

   Since we only have the latent heat at the reference condition temperature, we estimate the enthalpy at the boiling condition using Watson’s law

   \[h_{L,n}(T^*_{b,n}) = h_{L,n}(T^*) \left(\frac{T_{c,n} - T^*}{T_{c,n} - T^*_{b,n}} \right)^{-0.38}\]

3. Compute the latent heat of the droplet using

   \[h_{L,n}(T_d) = h_{g,n}(T_d) - h_{g,n}(T^*) + h_{L,n}(T^*) - c_{p,L,n}(T^*) (T_d - T^*) \,.\]

   and the saturation pressure, \(p_{{\rm{sat}}, n}\), using one of the methods described in the Liquid Spray Properties section.

4. Estimate the mass fractions in the vapor state using Raoult’s law

   \[ \begin{align}\begin{aligned}Y_{v,n} &= \frac{\chi_{v,n} M_n}{\overline{M}_v + \overline{M}_g (1 - \chi_{v,{\rm{sum}}})} \; \forall n \in N_L\\\chi_{v,{\rm{sum}}} &= \sum^{N_L}_{n=0} \chi_{v,n}\\\chi_{v,n} &= \frac{\chi_{d,n} p_{{\rm{sat}},n}}{p_g}\\\chi_{d,n} &= \frac{Y_{d,n}}{M_n}\left(\sum^{N_L}_{k=0} \frac{Y_{d,k}}{M_k}\right)^{-1}\\\overline{M}_v &= \sum^{N_L}_{n=0} \chi_{v,n} M_n\end{aligned}\end{align} \]

   If \(\chi_{g,n} p_g > p_{{\rm{sat}},n}\), then \(\chi_{v,n} = Y_{v,n} = 0\) for that particular species in the equations above, since that means the gas phase is saturated. The mass fractions in the reference state for the fuel are computed using the one-third rule and the remaining reference mass fractions are normalized gas phase mass fractions to ensure they sum to 1

   \[\begin{split}Y_{r,n} = \left\{\begin{array}{c l} \displaystyle Y_{v,n} + A (Y_{g,n} - Y_{v,n}) & {\text{If $Y_{v,n} > 0$}}, \\ \displaystyle\frac{1 - \sum^{N_L}_{k=0} Y_{v,k}}{1 - \sum^{N_L}_{k=0} Y_{g,k}} Y_{g,n} & {\text{Otherwise}}. \end{array}\right. \; \forall n \in N_s.\end{split}\]

5. The average molar mass, specific heat, and density of the reference state in the gas film are computed as

   \[ \begin{align}\begin{aligned}\overline{M}_r &= \left(\sum^{N_s}_{n=0} \frac{Y_{r,n}}{M_n}\right)^{-1},\\c_{p,r} &= \sum^{N_s}_{n=0} Y_{s,n} c_{p,g,n}(T_r),\\\rho_r &= \frac{\overline{M}_r p_g}{\mathcal{R} T_r}.\end{aligned}\end{align} \]

6. Transport properties are computed using the reference state: dynamic viscosity, \(\mu_r\), thermal conductivity, \(\lambda_r\), and mass diffusion coefficient for species \(n\), \(D_{r,n}\).

7. It is important to note that PelePhysics provides mixture averaged mass diffusion coefficient \(\overline{(\rho D)}_{r,n}\), which is converted into the binary mass diffusion coefficient using

   \[(\rho D)_{r,n} = \overline{(\rho D)}_{r,n} \overline{M}_r / M_n.\]

   Mass diffusion coefficient is then normalized by the total fuel vapor molar fraction

   \[(\rho D)^*_{r,n} = \frac{\chi_{v,n} (\rho D)_{r,n}}{\chi_{v,{\rm{sum}}}} \; \forall n \in N_L\]

   and the total is

   \[(\rho D)_r = \sum_{n=0}^{N_L} (\rho D)_{r,n}^*\]

8. The momentum source is a function of the drag force

   \[\mathbf{F}_d = \frac{1}{2} \rho_r C_D A_d \left\|\Delta \mathbf{u}\right\| \Delta \mathbf{u}\]

   where \(\Delta \mathbf{u} = \mathbf{u}_g - \mathbf{u}_d\), \(A_d = \pi d_d^2/4\) is the frontal area of the droplet, and \(C_D\) is the drag coefficient for a sphere, which is estimated using the standard drag curve for an immersed sphere

   \[\begin{split}C_D = \frac{24}{{\rm{Re}}_d}\left\{\begin{array}{c l} 1 & {\text{If Re$_d$ < 1}}, \\ \displaystyle 1 + \frac{{\rm{Re}}^{2/3}_d}{6} & {\text{Otherwise}}. \end{array}\right.\end{split}\]

   The droplet Reynolds number is defined as

   \[{\rm{Re}}_d = \frac{\rho_r d_d \left\|\Delta \mathbf{u}\right\|}{\mu_r}\]

9. The mass source term is modeled according to Abramzon and Sirignano (1989). The following non-dimensional numbers and factors are used:

   \[ \begin{align}\begin{aligned}F(B) &= (1 + B)^{0.7}\frac{\log(1 + B)}{B}\\F_2 &= \max(1, \min(400, {\rm{Re}}_d)^{0.077})\\{\rm{Pr}}_r &= \frac{\mu_r c_{p,r}}{\lambda_r}\\{\rm{Sc}}_r &= \frac{\mu_r}{(\rho D)_r}\\{\rm{Sh}}_0 &= 1 + (1 + {\rm{Re}}_d {\rm{Sc}}_r)^{1/3} F_2\\{\rm{Nu}}_0 &= 1 + (1 + {\rm{Re}}_d {\rm{Pr}}_r)^{1/3} F_2\\{\rm{Sh}}^* &= 2 + \frac{{\rm{Sh}}_0 - 2}{F(B_M)}\\{\rm{Nu}}^* &= 2 + \frac{{\rm{Nu}}_0 - 2}{F(B_T)}\end{aligned}\end{align} \]

   • The Spalding numbers for mass transfer, \(B_M\), and heat transfer, \(B_T\), are computed using

     \[ \begin{align}\begin{aligned}B_M &= \displaystyle\frac{\sum^{N_L}_{n=0} Y_{v,n} - \sum^{N_L}_{n=0} Y_{g,n}}{1 - \sum^{N_L}_{n=0} Y_{v,n}}\\B_T &= \left(1 + B_M\right)^{\phi} - 1\end{aligned}\end{align} \]

     where

     \[\phi = \frac{c_{p,r} (\rho D)_r {\rm{Sh}}^*}{\lambda_r {\rm{Nu}}^*}\]

     Note the dependence of \({\rm{Nu}}^*\) on \(B_T\) means an iterative scheme is required to solve for both. The droplet vaporization rate and heat transfer become

     \[ \begin{align}\begin{aligned}\dot{m}_n &= -\pi (\rho D)_{r,n}^* d_d {\rm{Sh}}^* \log(1 + B_M). \; \forall n \in N_L\\\mathcal{Q}_d &= \pi \lambda_r d_d (T_g - T_d) {\rm{Nu}}^* \frac{\log(1 + B_T)}{B_T}\end{aligned}\end{align} \]

   • If the gas phase is saturated for all liquid species, the equations for heat and mass transfer become

     \[ \begin{align}\begin{aligned}\dot{m}_n &= 0\\\mathcal{Q}_d &= \pi \lambda_r d_d (T_g - T_d) {\rm{Nu}}_0\end{aligned}\end{align} \]

10. To alleviate conservation issues at AMR interfaces, each parcel only contributes to the gas phase source term of the cell containing it. The gas phase source terms for a single parcel to the cell are

    \[ \begin{align}\begin{aligned}S_{\rho} &= \mathcal{C} \sum^{N_L}_{n=0} \dot{m}_n,\\S_{\rho Y_n} &= \mathcal{C} \dot{m}_n,\\\mathbf{S}_{\rho \mathbf{u}} &= \mathcal{C} \mathbf{F}_d,\\S_{\rho h} &= \mathcal{C}\left(\mathcal{Q}_d + \sum_{n=0}^{N_L} \dot{m}_n h_{g,n}(T_d)\right),\\S_{\rho E} &= S_{\rho h} + \frac{1}{2}\left\|\mathbf{u}_d\right\| S_{\rho} + \mathcal{C} \mathbf{F}_d \cdot \mathbf{u}_d\end{aligned}\end{align} \]

    where

    \[\mathcal{C} = -\frac{N_{d}}{V_{\rm{cell}}},\]

    \(N_{d}\) is the number of droplets per computational parcel, and \(V_{\rm{cell}}\) is the volume for the cell of interest. Note that the cell volume can vary depending on AMR level and if an EB is present.

Warning

Dimensional Assumptions in the Spray Model

The spray model assumes spherically symmetric droplets and is inherently three-dimensional. For two-dimensional simulations, the domain is treated as one cell wide in the \(z\)-direction, with \(L_z = \Delta x\), so the volume in the gas-phase source terms is:

\[V_{\rm{cell}} = \Delta x \, \Delta y \, \Delta x\]

For nominally single droplet cases, this effectively places an infinite array of droplets spaced \(\Delta x\) apart in \(z\), exaggerating Stefan flow in the \(x\)- and \(y\)-directions and omitting flow in \(z\). While this has minimal impact on droplet diameter or temperature, it can distort the surrounding gas-phase flow, especially for low \(\text{Re}_d\).

For such cases, fully three-dimensional simulations are recommended.

Spray Flags and Inputs

• In the GNUmakefile, specify USE_PARTICLES = TRUE and SPRAY_FUEL_NUM = N where N is the number of liquid species being used in the simulation.

• Depending on the gas phase solver, spray solving functionality can be turned on in the input file using pelec.do_spray_particles = 1 or peleLM.do_spray_particles = 1.

• There are many required particles. flags in the input file. For demonstration purposes, 2 liquid species of NC7H16 and NC10H22 will be used.

  • The liquid fuel species names are specified using particles.fuel_species = NC7H16 NC10H22. The number of fuel species listed must match SPRAY_FUEL_NUM.

  • Although this is not required or typical, if the evaporated mass should contribute to a different gas phase species than what is modeled in the liquid phase, use particles.dep_fuel_species. For example, if we wanted the evaporated mass from both liquid species to contribute to a different species called SP3, we would put particles.dep_fuel_species = SP3 SP3. All species specified must be present in the chemistry transport and thermodynamic data.

• The following table lists other inputs related to particles.

Input	Description	Required	Default Value
fuel_species	Names of liquid species	Yes	None
dep_fuel_species	Name of gas phase species to contribute	Yes	Inputs to fuel_species
mom_transfer	Couple momentum with gas phase	No	1
mass_transfer	Evaporate mass and exchange heat with gas phase	No	1
fixed_parts	Fix particles in space	No	0
parcel_size	\(N_{d}\); Number of droplets per parcel	No	1.
write_ascii_files	Output ascii files of spray data	No	0
cfl	Particle CFL number for limiting time step	No	0.5
init_file	Ascii file name to initialize droplets	No	Empty

Liquid Spray Properties

The required inputs and corresponding correlations for the original PeleMP [1] and the FuelLib-based GCM are outlined in the subsections below. Please note the following details:

Units:

• PeleLM and PeleLMeX use MKS units, while PeleC uses CGS units. The Spray inputs follow the same convention.

• For example, when running a spray simulation coupled with PeleC, the values for particles.fuel_cp must be provided in erg/g.

Input flags:

• A number of particles. flags are required in the input file to define liquid fuel properties.

• For demonstration purposes, two liquid species will be used: NC7H16 and NC10H22.

• Many values must be specified on a per-species basis. In this example, one would need to specify:

  • particles.NC7H16_crit_temp = 540 critical temperature of 540 K for NC7H16

  • particles.NC10H22_crit_temp = 617 critical temperatures of 617 K for NC10H22.

Additional method-specific inputs:

• The following tables list other required inputs related to particles., where SP refers to a given fuel species name.

The source code for the liquid spray properties can be found in SprayProperties.H.

PeleMP Implementation

Input	Description	Required	Default Value
fuel_ref_temp	Liquid reference temperature	Yes	None
SP_crit_temp	Critical temperature	Yes	None
SP_boil_temp	Boiling temperature at atmospheric pressure	Yes	None
SP_cp	Liquid \(c_p\) at reference temperature	Yes	None
SP_latent	Latent heat at reference temperature	Yes	None
SP_rho	Liquid density	Yes	None
SP_lambda	Liquid thermal conductivity	No
SP_mu	Liquid dynamic viscosity	No
SP_sigma	Liquid surface tension	No

• If an Antoine fit for saturation pressure is used, it must be specified for individual species,

  particles.SP_psat = 4.07857 1501.268 -78.67 1.E5
  

  where the numbers represent coefficients \(a_n\), \(b_n\), \(c_n\), and unit conversion \(d_n\), respectively in:

  \[p_{\rm{sat},n}(T) = d_n 10^{a_n - b_n / (T + c_n)}.\]

  • If no fit is provided, the saturation pressure is estimated using the Clasius-Clapeyron relation

    \[p_{{\rm{sat}}, n} = p_{\rm{atm}} \exp\left(\frac{h_{L,n}(T_d) M_n}{\mathcal{R}} \left(\frac{1}{T^*_{b,n}} - \frac{1}{T_d}\right)\right)\]

• Temperature based fits for liquid density, thermal conductivity, and dynamic viscosity can be used; these can be specified as

  particles.SP_rho = 10.42 -5.222 1.152E-2 4.123E-7
  particles.SP_lambda = 7.243 1.223 4.223E-8 8.224E-9
  particles.SP_mu = 7.243 1.223 4.223E-8 8.224E-9
  

  where the numbers represent \(a_n\), \(b_n\), \(c_n\), and \(d_n\), respectively in:

  \[ \begin{align}\begin{aligned}\rho_{L,n} \,, \lambda_{L,n} = a_n + b_n T + c_n T^2 + d_n T^3\\\mu_{L,n} = a_n + b_n / T + c_n / T^2 + d_n / T^3\end{aligned}\end{align} \]

  If only a single value is provided, \(a_n\) is assigned to that value and the other coefficients are set to zero, effectively using a constant value for the parameters.

FuelLib-Based GCM

Currently the GCM approach of estimating liquid fuel properties is only available in PeleLMeX and requires:

• Setting the compile-time flag SPRAY_GCM=TRUE in the case’s GNUmakefile

• Generating a liquid-fuel-specific GCM input file from FuelLib, and copying the input file into the case directory.

  • The process for generating this input file is provided in FuelLib’s tutorial: Exporting GCM Properties for Pele.

  • An example of using the GCM in Pele is provided in PeleLMeX/Exec/RegTests/SingleDropEvap.

The following inputs are generated from FuelLib for each liquid fuel species.

Input	Description	Required
SP_family	Compound family	Yes
SP_molar_weight	Molecular weight	Yes
SP_crit_temp	Critical temperature	Yes
SP_crit_press	Critical pressure	Yes
SP_crit_vol	Critical volume	Yes
SP_boil_temp	Boiling temperature at atmospheric pressure	Yes
SP_accentric_factor	Critical temperature	Yes
SP_molar_vol	Molecular volume	Yes
SP_cp_a, SP_cp_c, SP_cp_c	GCM coefficients for specific heat	Yes
SP_latent	Latent heat at 298.15 K	Yes

The specific equations, correlations and mixture rules used in the GCM implementation are detailed in the Fuel Property Prediction Model section of FuelLib’s documentation.

Spray Injection

Templates to facilitate and simplify spray injection are available. To use them, changes must be made to the input and SprayParticlesInitInsert.cpp files. Inputs related to injection use the spray. parser name. To create a jet in the domain, modify the InitSprayParticles() function in SprayParticleInitInsert.cpp. Here is an example:

void
SprayParticleContainer::InitSprayParticles(
const bool init_parts)
{
  int num_jets = 1;
  m_sprayJets.resize(num_jets);
  std::string jet_name = "jet1";
  m_sprayJets[0] = std::make_unique<SprayJet>(jet_name, Geom(0));
  return;
}

This creates a single jet that is named jet1. This name will be used in the input file to reference this particular jet. For example, to set the location of the jet center for jet1, the following should be included in the input file,

spray.jet1.jet_cent = 0. 0. 0.

No two jets may have the same name. If an injector is constructed using only a name and geometry, the injection parameters are read from the input file. Here is a list of injection related inputs:

Input	Description	Required
jet_cent	Jet center location	Yes
jet_norm	Jet normal direction	Yes
jet_vel	Jet velocity magnitude	Yes
jet_dia	Jet diameter	Yes
spread_angle	\(\theta_J\); Full spread angle in degrees from the jet normal direction; droplets vary from \([-\theta_J/2,\theta_J/2]\)	Yes
T	Temperature of the injected liquid	Yes
Y	Mass fractions of the injected liquid based on particles.fuel_species	Yes, if SPRAY_FUEL_NUM > 1
mass_flow_rate	\(\dot{m}_{\rm{inj}}\); Mass flow rate of the jet	Yes
hollow_spray	Sets hollow cone injection with angle \(\theta_J/2\)	No (Default: 0)
hollow_spread	\(\theta_h\); Adds spread to hollow cone \(\theta_J/2\pm \theta_h\)	No (Default: 0)
swirl_angle	\(\phi_S\); Adds a swirling component along azimuthal direction	No (Default: 0)
start_time and end_time	Beginning and end time for jet	No
dist_type	Droplet diameter distribution type: Uniform, Normal, LogNormal, Weibull, ChiSquared	Yes

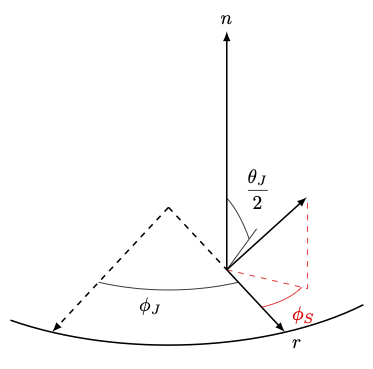
9 Demonstration of injection angles. \(\phi_J\) varies uniformly from \([0, 2 \pi]\)

Care must be taken to ensure the amount of mass injected during a time step matches the desired mass flow rate. For smaller time steps, the risk of over-injecting mass increases. To mitigate this issue, each jet accounts for three values: \(N_{P,\min}\), \(m_{\rm{acc}}\), and \(t_{\rm{acc}}\) (labeled in the code as m_minParcel, m_sumInjMass, and m_sumInjTime, respectively). \(N_{P,\min}\) is the minimum number of parcels that must be injected over the course of an injection event; this must be greater than or equal to one. \(m_{\rm{acc}}\) is the amount of uninjected mass accumulated over the time period \(t_{\rm{acc}}\). The injection routine steps are as follows:

1. The injected mass for the current time step is computed using the desired mass flow rate, \(\dot{m}_{\rm{inj}}\) and the current time step

   \[m_{\rm{inj}} = \dot{m}_{\rm{inj}} \Delta t + m_{\rm{acc}}\]

2. The time period for the current injection event is computed using

   \[t_{\rm{inj}} = \Delta t + t_{\rm{acc}}\]

3. Using the average mass of an injected parcel, \(N_{d} m_{d,\rm{avg}}\), the estimated number of injected parcels is computed

   \[N_{P, \rm{inj}} = m_{\rm{inj}} / (N_{d} m_{d, \rm{avg}})\]

• If \(N_{P, \rm{inj}} < N_{P, \min}\), the mass and time is accumulated as \(m_{\rm{acc}} = m_{\rm{inj}}\) and \(t_{\rm{acc}} = t_{\rm{inj}}\) and no injection occurs this time step.

• Otherwise, \(m_{\rm{inj}}\) mass is injected and convected over time \(t_{\rm{inj}}\) and \(m_{\rm{acc}}\) and \(t_{\rm{acc}}\) are reset.

4. If injection occurs, the amount of mass injected, \(m_{\rm{actual}}\), is summed and compared with the desired mass flow rate. If \(m_{\rm{actual}} / t_{\rm{inj}} - \dot{m}_{\rm{inj}} > 0.05 \dot{m}_{\rm{inj}}\), then \(N_{P,\min}\) is increased by one to reduce the likelihood of over-injecting in the future. A balance is necessary: the higher the minimum number of parcels, the less likely to over-inject mass but the number of time steps between injections can potentially grow as well.

Spray data derived from ANSYS Fluent DPM solution files can also be used to inject spray particles into the fluid domain. To use this feature, initialize a spray jet (named jet_dpm, say) by using the statement spray.jetnames=jet_dpm in the input file as previously mentioned. In order to use the ANSYS Fluent DPM capability, set the boolean input variable spray.jet_dpm.read_from_dpm_file to true and specify the DPM file name by spray.jet_dpm.dpm_filename=<filename>. The DPM data in the file will correspond to a specified time-gap, but it can be made to repeat periodically by specifying spray.jet_dpm.is_dpm_periodic=true. Otherwise, spray particle injection will cease after the final DPM time is reached. The spray injection can be set to start from a specific DPM time stamp by specifying spray.jet_dpm.initial_injection_dpm_time=<DPM time stamp>. Similarly, the spray injection can also be set to start from a specific flow time by setting spray.jet_dpm.initial_injection_flow_time to the appropriate value. If the coordinate system used in the ANSYS Fluent DPM file is different from that in Pele, one can use spray.jet_dpm.trans_matrix and spray.jet_dpm.translation to specify the direction cosine matrix (3X3 matrix) and the translation vector (<dx,dy,dz>) to align both the coordinate systems.

The DPM file has a specific format and a typical file is shown below:

Spray Validation

Single Droplet Tests

Single droplet tests are performed in 2D with PeleLMeX and compared with experimental results published in literature. These tests are setup in PeleLMeX/Exec/RegTests/SingleDropEvap and can be compiled with SPRAY_GCM=TRUE or FALSE. To run a test case with the PeleMP or GCM liquid properties, simply open Validate.py and set the variables for case_name, LiqPropsType, and the method for calculating \(p_{\rm sat}\) for the PeleMP model. For example

case_name = "WongLin"
LiqPropsType = "gcm"

# Psat model for PeleMP: "Antoine" or "Clasius-Clapeyron"
PeleMP_PsatModel = "Antoine"

then run python Validate.py. The following table details the parameters of each test:

Test Name	\(T_g\) [K]	\(p_g\) [bar]	\(T_d\) [K]	\(d_d\) [um]	\(\Delta u\) [m/s]	Fuel	Ref
Nomura	471	1	298	700	0.0	heptane	[8]
WongLin	1000	1.01325	315	1961	0.385	decane	[9]
Daif	348	1.01325	291	1334	3.1	heptane/decane	[10]
RungeHep, RungeDec, RungeMix	272	1.01325	272	570-594	2.5	heptane, decane, mix	[11]
RungeJP8	294.15	1.01325	294.15	636	3.0	POSF10264	[11]

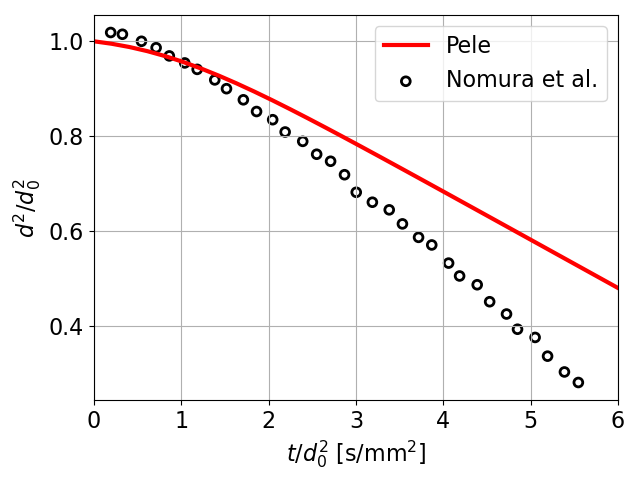
10 Heptane droplet diameter comparisons with Nomura et al. [8]

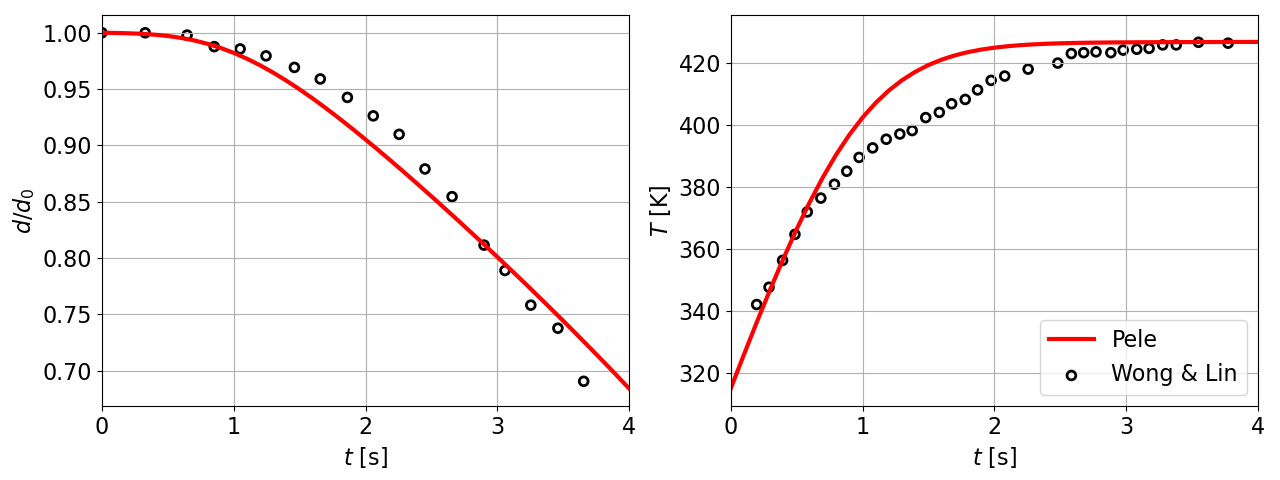
11 Decane droplet diameter and temperature comparisons with Wong & Lin [9]

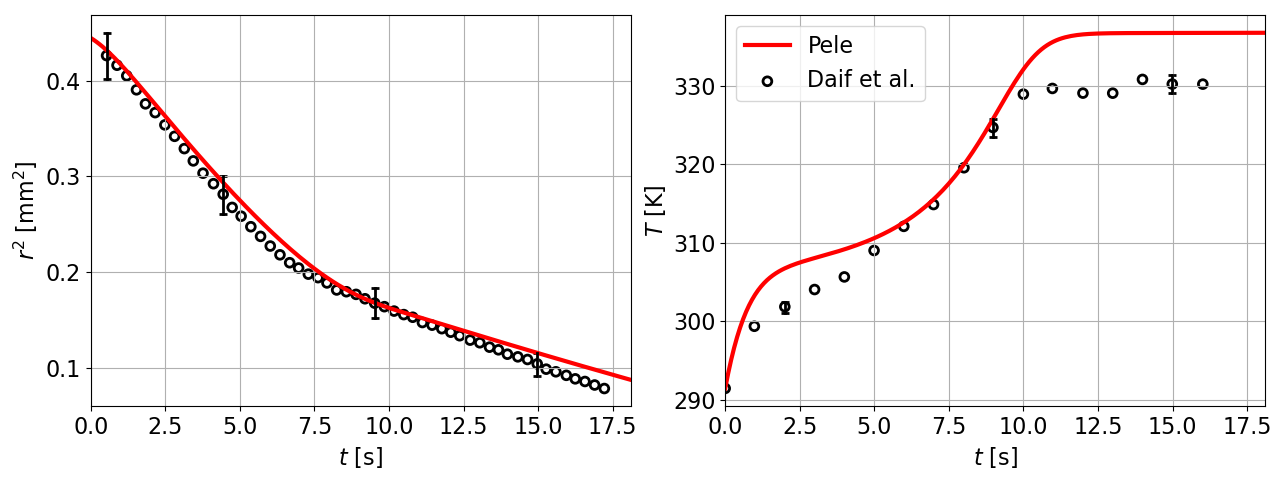
12 Binary mixture of heptane and decane droplet diameter and temperature comparisons with Daı̈f et al. [10]

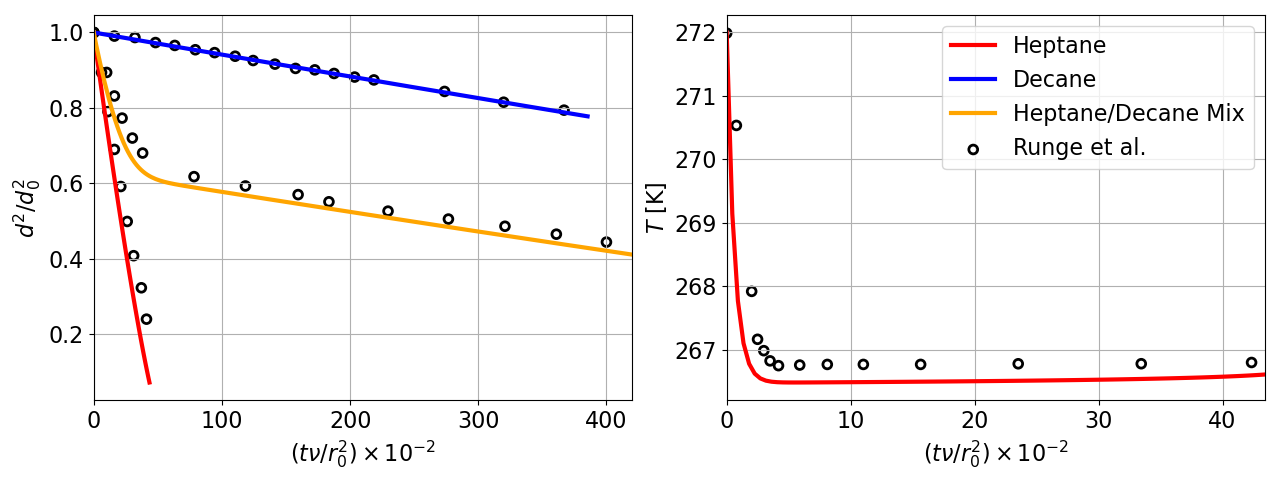
13 Droplet evaporation of heptane, decane, and a binary mixture of heptane and decane compared to experimental measurements from with Runge et al. [11] All three PeleMP cases utilized an Antoine fit for estimating the saturated vapor pressure.

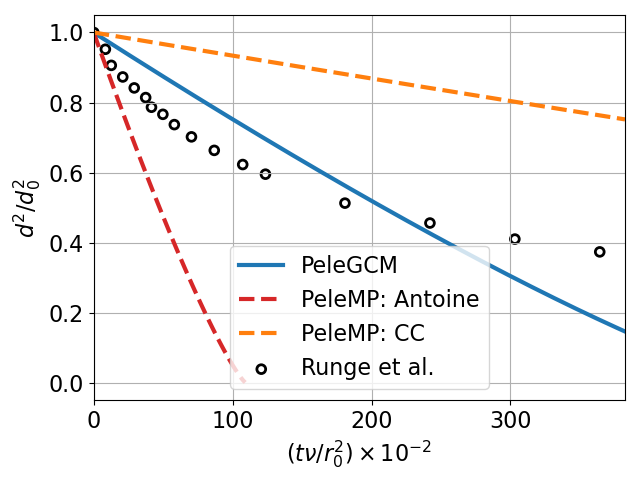
14 Droplet evaporation of POSF10264 (JP8) compared to experimental measurements from with Runge et al. [11] Note that all three cases represent a multicomponent fuel with a single liquid-phase and single gas-phase species.

[1] (1,2)

“PeleMP: The Multiphysics Solver for the Combustion Pele Adaptive Mesh Refinement Code Suite,” L. D. Owen, W. Ge, M. Rieth, M. Arienti, L. Esclapez, B. S. Soriano, M. E. Mueller, M. Day, R. Sankaran, and J. H. Chen, J. Fluids Eng., vol. 146, no. 4, pp. 1-18 (2024), doi: 10.1115/1.4064494.

[2]

“New group contribution method for estimating properties of pure compounds”, L. Constantinou, and R. Gani, AIChE J., Vol. 40, No. 10, pp.1697-1710 (1994), doi: 10.1002/aic.690401011.

[3]

“Estimation of the acentric factor and the liquid molar volume at 298 K using a new group contribution method”, L. Constantinou, and R. Gani, Fluid Phase Equilibria, Vol. 103, No. 1, pp.11-22 (1995), doi: 10.1016/0378-3812(94)02593-P..

[4]

“Group contribution method for multicomponent evaporation with application to transportation fuels”, Int. J. of Heat and Mass Transfer, Vol. 102, pp.833–845 (2016), doi: 10.1016/j.ijheatmasstransfer.2016.06.079.

[5]

“Droplet vaporization model for spray combustion calculations”, B. Abramzon and W. A. Sirignano, Int. J. Heat Mass Transfer, vol. 32, no. 9, pp. 1605-1618 (1989), doi: 10.1016/0017-9310(89)90043-4.

[6]

“Fuel spray modeling in direct-injection diesel and gasoline engines”, S. Tonini, Dissertation, City University London (2006), url: https://openaccess.city.ac.uk/id/eprint/8486/.

[7]

“Development of a CPU/GPU portable software library for Lagrangian-Eulerian simulations of liquid sprays”, W. Ge and R. Sankaran and J. H. Chen, Int. J. Multiph. Flow, vol. 128 (2020), doi: 10.1016/j.ijmultiphaseflow.2020.103293.

[8] (1,2)

“Experimental study on high-pressure droplet evaporation using microgravity conditions”, H. Nomura and Y. Ujiie and H. J. Rath and J. Sato and M. Kono, Symposium (International) on Combustion, vol. 26, no. 1, pp. 1267–1273 (1996), doi: 10.1016/S0082-0784(96)80344-4.

[9] (1,2)

“Internal temperature distributions of droplets vaporizing in high-temperature convective flows”, S.-C. Wong and A.-C. Lin, J. Fluid Mech., vol. 237, pp. 671–687 (1992), doi: 10.1017/S0022112092003574.

[10] (1,2)

“Comparison of multicomponent fuel droplet vaporization experiments in forced convection with the Sirignano model”, A. Daı̈f and M. Bouaziz and X. Chesneau and A. Ali Chérif, Exp. Therm. Fluid Sci., vol. 18, no. 4, pp. 282-290, Issn 0894-1777 (1998), doi: 10.1016/S0894-1777(98)10035-3.

[11] (1,2,3,4)

“Low-temperature vaporization of JP-4 and JP-8 fuel droplets”, T. Runge and M. Teske and C. E. Polymeropoulos, At. Sprays, vol. 8, pp. 25-44 (1998), doi: 10.1615/AtomizSpr.v8.i1.20.