Non-reacting flow past a cylinder
Introduction
PeleLMeX enables the representation of complex non-Cartesian geometries using an embedded boundary (EB) method. This method relies on intersecting an arbitrary surface with the Cartesian matrix of uniform cells, and modifies the numerical stencils near cells that are cut by the EB.
The goal of this EB_FlowPastCylinder tutorial is to setup a simple 2-dimentional flow past cylinder case in PeleLMeX.
This document provides step by step instructions to properly set-up the domain and boundary conditions,
construct an initial solution.
Setting-up your environment
Getting a functioning environment in which to compile and run PeleLMeX is the first step of this tutorial. Follow the steps listed below to get to this point:
The first step is to get PeleLMeX and its dependencies. To do so, use a recursive git clone:
git clone --recursive --shallow-submodules --single-branch https://github.com/AMReX-Combustion/PeleLMeX.git
The
--shallow-submodulesand--single-branchflags are recommended for most users as they substantially reduce the size of the download by skipping extraneous parts of the git history. Developers may wish to omit these flags in order download the complete git history of PeleLMeX and its submodules, though standardgitcommands may also be used after a shallow clone to obtain the skipped portions if needed.Move into the Exec folder containing your tutorial. To do so:
cd PeleLMeX/Exec/RegTests/<CaseName>
where <CaseName> is the name of your tutorial, e.g.
HotBubble,FlameSheet,EB_BackwardStepFlame,EB_FlowPastCylinder, orTripleFlame.
You’re good to go!
Note
The makefile system is set up such that default paths are automatically set to the submodules obtained with the recursive git clone, however advanced users can set their own dependencies in the GNUmakefile for each case by updating the top-most lines as follows:
PELE_HOME = <path_to_PeleLMeX>
AMREX_HOME = <path_to_MyAMReX>
AMREX_HYDRO_HOME = <path_to_MyAMReXHydro>
PELE_PHYSICS_HOME = <path_to_MyPelePhysics>
SUNDIALS_HOME = <path_to_MySUNDIALS>
or directly through shell environment variables (using bash for instance):
export PELE_HOME=<path_to_PeleLMeX>
export AMREX_HOME=<path_to_MyAMReX>
export AMREX_HYDRO_HOME=<path_to_MyAMReXHydro>
export PELE_PHYSICS_HOME=<path_to_MyPelePhysics>
export SUNDIALS_HOME=<path_to_MySUNDIALS>
Note that using the first option will overwrite any environment variables you might have previously defined when using this GNUmakefile.
Numerical setup
In this section we review the content of the various input files for the flow past cylinder test case. To get additional information about the keywords discussed, the user is referred to PeleLMeX controls.
Test case and boundary conditions
Direct Numerical Simulations (DNS) is performed on a 12x4 \(cm^2\) 2D computational domain, with the bottom left corner located at (-0.02:-0.02) and the top right corner at (0.10:0.02). The base grid is decomposed into 192x64 cells and up to 3 levels of refinement (although we will start with a single level). The refinement ratio between each level is set to 2. The maximum box size is fixed at 64, and the base (level 0) grid is composed of 3 boxes, as shown in Fig. 14.
Periodic boundary conditions are used in the transverse (\(y\)) direction, while Inflow (dirichlet) and Outflow (neumann) boundary conditions are used in the main flow direction (\(x\)). The flow goes from left to right.
A cylinder of radius 0.0035 m is placed in the middle of the flow at (0.0:0.0).
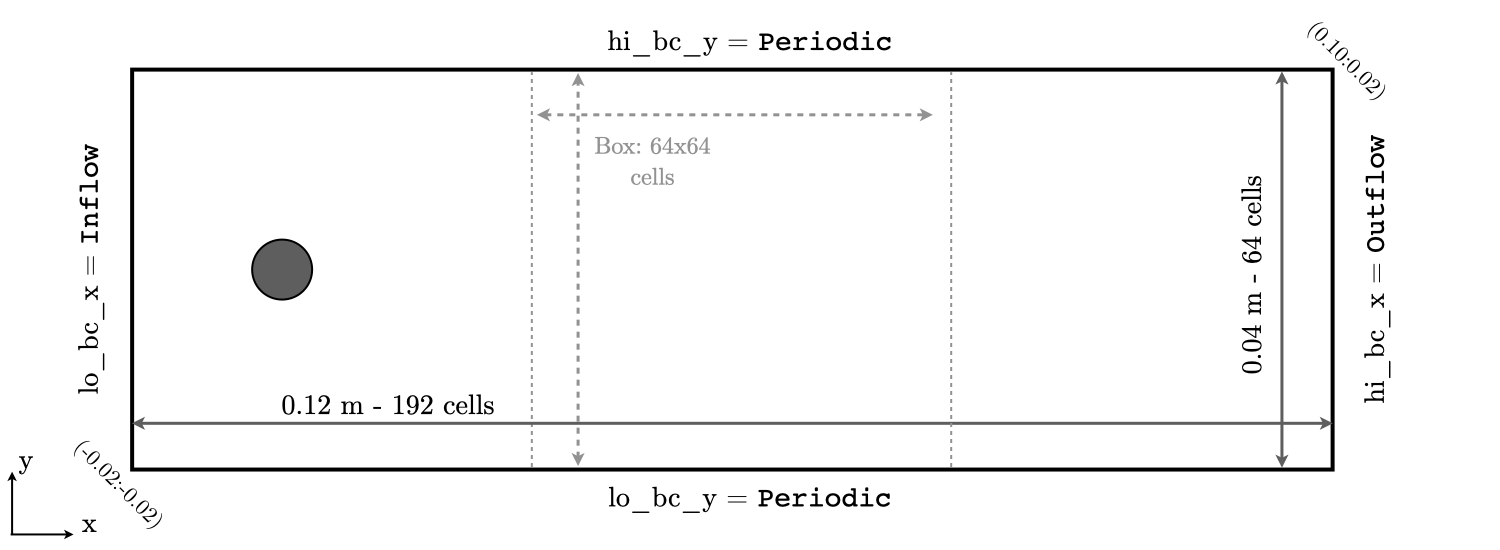
Fig. 14 : Sketch of the computational domain with level 0 box decomposition.
The geometry of the problem is specified in the first block of the input.2d-Re500:
#----------------------DOMAIN DEFINITION------------------------
geometry.is_periodic = 0 1 # Periodicity in each direction: 0 => no, 1 => yes
geometry.coord_sys = 0 # 0 => cart, 1 => RZ
geometry.prob_lo = -0.02 -0.02 # x_lo y_lo
geometry.prob_hi = 0.10 0.02 # x_hi y_hi
The second block determines the boundary conditions. Note that Interior is used to indicate periodic boundary conditions. Refer to Fig. 14:
#--------------------------BC FLAGS-----------------------------
# Interior, Inflow, Outflow, Symmetry,
# SlipWallAdiab, NoSlipWallAdiab, SlipWallIsotherm, NoSlipWallIsotherm
peleLM.lo_bc = Inflow Interior
peleLM.hi_bc = Outflow Interior
In the present case, the EB geometry is a simple cylinder (or sphere) which is readily available from the AMReX library and only a few parameters need to be specified by the user. This is done further down in the input file:
#------------------------- EB SETUP -----------------------------
eb2.geom_type = sphere
eb2.sphere_radius = 0.005
eb2.sphere_center = 0.00 0.00
eb2.sphere_has_fluid_inside = 0
eb2.small_volfrac = 1.0e-4
Note that the last parameter is used to specify a volume fraction (ratio of the uncovered surface (2D) or volume (3D) over the cell surface or volume) threshold below which a cell is considered fully covered. This prevents the appearance of extremely small partially covered cells which are numerically unstable.
The number of levels, refinement ratio between levels, maximum grid size as well as other related refinement parameters are set under the third block :
#-------------------------AMR CONTROL----------------------------
amr.n_cell = 192 64 # Level 0 number of cells in each direction
amr.v = 1 # amr verbosity level
amr.max_level = 0 # maximum level number allowed
amr.ref_ratio = 2 2 2 2 # refinement ratio
amr.regrid_int = 5 # how often to regrid
amr.n_error_buf = 2 2 2 2 # number of buffer cells in error est
amr.grid_eff = 0.7 # what constitutes an efficient grid
amr.blocking_factor = 16 # block factor in grid generation
amr.max_grid_size = 64 # maximum box size
Problem specifications
This very simple problem only has three user-defined problem parameters: the inflow velocity magnitude, the pressure and the temperature.
Specifying dirichlet Inflow conditions in PeleLMeX can seem daunting at first. But it is actually a very flexible process. We walk the user through the details which involve the following files:
pelelmex_prob.H, contains in two C++ structs:MyProbParmencapsulates the input variables as well as other variables used in the initialization process andMyProblemSpecificFunctionsgathers the functions responsible for generating the initial and boundary conditions (amongst others),initdataandbcnormal.pelelmex_prob.cpp, initialize and provide default values to the entries ofMyProbParmand allow the user to pass run-time value using the AMReX parser (ParmParse). In the present case, the parser will read the parameters in theProblemblock:#--------------------------- Problem ------------------------------- prob.T_mean = 300.0 prob.P_mean = 101325.0 prob.meanFlowMag = 4.255 prob.meanFlowDir = 1
Finally, this test uses a constant set of transport parameters rather relying on the Simple library. These transport parameters are specified in the CONSTANT TRANSPORT block:
#------------ INPUTS TO CONSTANT TRANSPORT -----------------
transport.units = MKS
transport.const_viscosity = 1.0e-04
transport.const_bulk_viscosity = 0.0
transport.const_conductivity = 0.0
transport.const_diffusivity = 0.0
Only the viscosity in the present case. Using these parameters, it is possible to evaluate the Reynolds number, based on the inflow velocity and the cylinder diameter:
This relatively high value ensures that the flow will exhibit vortex shedding.
Initial solution
An initial field of the main variables is always required to start a simulation. In the present case, the computational domain is filled with air in the condition of pressure and temperature provided by the user (or the default ones). An initial constant velocity of meanFlowMag is used, but note that PeleLMeX performs an initial velocity projection to enforce the low Mach number constraint which overwrite this initial velocity.
This initial solution is constructed via the routine MyProblemSpecificFunctions::initdata(), in the file pelelmex_prob.H. Additional information is provided as comments in this file for the eager reader, but nothing is required from the user at this point.
Numerical scheme
The NUMERICS CONTROL block can be modified by the user to increase the number of SDC iterations. Note that there are many other parameters controlling the numerical algorithm that the advanced user can tweak, but we will not talk about them in the present Tutorial. The interested user can refer to PeleLMeX controls.
Building the executable
The last necessary step before starting the simulation consists of building the PeleLMeX executable. AMReX applications use a makefile system to ensure that all the required source code from the dependent libraries be properly compiled and linked. The GNUmakefile provides some compile-time options regarding the simulation we want to perform.
The first few lines specify the paths towards the source code of PeleLMeX, AMReX, AMREX-Hydro and PelePhysics, and might have been already updated in Setting-up your environment earlier.
Next comes the build configuration block:
#
# Build configuration
#
# AMREX options
DIM = 2
USE_EB = TRUE
# Compiler / parallel paradigms
COMP = gnu
USE_MPI = TRUE
USE_OMP = FALSE
USE_CUDA = FALSE
USE_HIP = FALSE
USE_SYCL = FALSE
# MISC options
DEBUG = FALSE
PRECISION = DOUBLE
VERBOSE = FALSE
TINY_PROFILE = FALSE
It allows the user to specify the number of spatial dimensions (2D), trigger the compilation of the EB source code, the compiler (gnu) and the parallelism paradigm (in the present case only MPI is used). The other options can be activated for debugging and profiling purposes. Note that on OSX platform, one should update the compiler to llvm.
In PeleLMeX, the chemistry model (set of species, their thermodynamic and transport properties as well as the description of their of chemical interactions) is specified at compile time. Chemistry models available in PelePhysics can used in PeleLMeX by specifying the name of the folder in PelePhysics/Mechanisms containing the relevant files, for example:
Chemistry_Model = air
Here, the model air, only contains 2 species (O2 and N2). Advanced users may also specify
USE_CUSTOM_CHEMISTRY = TRUE, in which case Chemistry_Model is interpreted as a path and can point to models not included in
PelePhysics by default, though the new model directory must contain valid chemistry model files.
The user is referred to the PelePhysics documentation for a list of available mechanisms and more information regarding the EOS, chemistry and transport models specified:
Eos_Model := Fuego
Transport_Model := Constant
Finally, PeleLMeX utilizes the chemical kinetic ODE integrator CVODE. This Third Party Library (TPL) is shipped as a submodule of the PeleLMeX distribution and can be readily installed through the makefile system of PeleLMeX. To do so, type in the following command:
make -j4 TPL
Note that the installation of CVODE requires CMake 3.23.1 or higher.
You are now ready to build your first PeleLMeX executable !! Type in:
make -j4
The option here tells make to use up to 4 processors to create the executable (internally, make follows a dependency graph to ensure any required ordering in the build is satisfied). This step should generate the following file (providing that the build configuration you used matches the one above):
PeleLMeX2d.gnu.MPI.ex
You’re good to go!
Running the problem on a coarse grid
As a first step towards obtaining the classical Von-Karman alleys, we will now let the flow establish using only the coarse base grid. The simulation will last for 25 ms.
Time-stepping parameters in input.2d-Re500 are specified in the TIME STEPPING block:
#---------------------------TIME STEPPING---------------------------
amr.max_step = 300000 # Maximum number of time steps
amr.stop_time = 0.025 # final physical time
amr.cfl = 0.3 # cfl number for hyperbolic system
amr.dt_shrink = 0.1 # scale back initial timestep
amr.dt_change_max = 1.1 # maximum dt change
The final simulation time is set to 0.025 s. PeleLMeX solves for the advection, diffusion and reaction processes in time, but only the advection term is treated explicitly and thus it constrains the maximum time step size \(dt_{CFL}\). This constraint is formulated with a classical Courant-Friedrich-Levy (CFL) number, specified via the keyword amr.cfl.
Additionally, as it is the case here, the initial solution is often made-up by the user and local mixture composition and temperature can result in the introduction of unreasonably fast chemical scales.
To ease the numerical integration of this initial transient, the parameter amr.dt_shrink allows to shrink the initial dt (evaluated from the CFL constraint) by a factor (usually smaller than 1), and let it relax towards \(dt_{CFL}\) at a rate given by amr.dt_change_max as the simulation proceeds. Since the present case does not involve complex chemical processes, amr.dt_shrink is kept to relatively high value of 0.1.
Input/output from PeleLMeX are specified in the IO CONTROL block:
#-------------------------IO CONTROL----------------------------
amr.check_file = "chk_" # root name of checkpoint file
amr.check_per = 0.05 # frequency of checkpoints
amr.plot_file = "plt_" # root name of plotfiles
amr.plot_per = 0.005 # frequency of plotfiles
amr.derive_plot_vars = rhoRT mag_vort avg_pressure gradpx gradpy
Information pertaining to the checkpoint and plot_file files name and output frequency can be specified there.
We have specified here that a checkpoint file will be generated every 50 ms and a plotfile every 5 ms. PeleLMeX will always generate an initial plotfile plt_00000 if the initialization is properly completed, and a final plotfile at the end of the simulation. It is possible to request including derived variables in the plotfiles by appending their names to the amr.derive_plot_vars keyword. These variables are derived from the state variables (velocity, density, temperature, \(\rho Y_k\), \(\rho h\)) which are automatically included in the plotfile.
You finally have all the information necessary to run the first of several steps. Type in:
./PeleLMeX2d.gnu.MPI.ex input.2d-Re500
Some information is printed directly on the screen during a PeleLMeX simulation, but it will not be detailed in the present tutorial. If you wish to store these information for later analysis, you can instead use:
./PeleLMeX2d.gnu.MPI.ex input.2d-Re500 > logCoarseRun.dat &
Whether you have used one or the other command, the computation finishes within a couple of minutes and you should obtain a set of plt_**** files (and maybe a set appended with .old*********** if you used both commands). Use Amrvis to visualize the results. Use the following command to open the entire set of solutions:
amrvis -a plt_?????
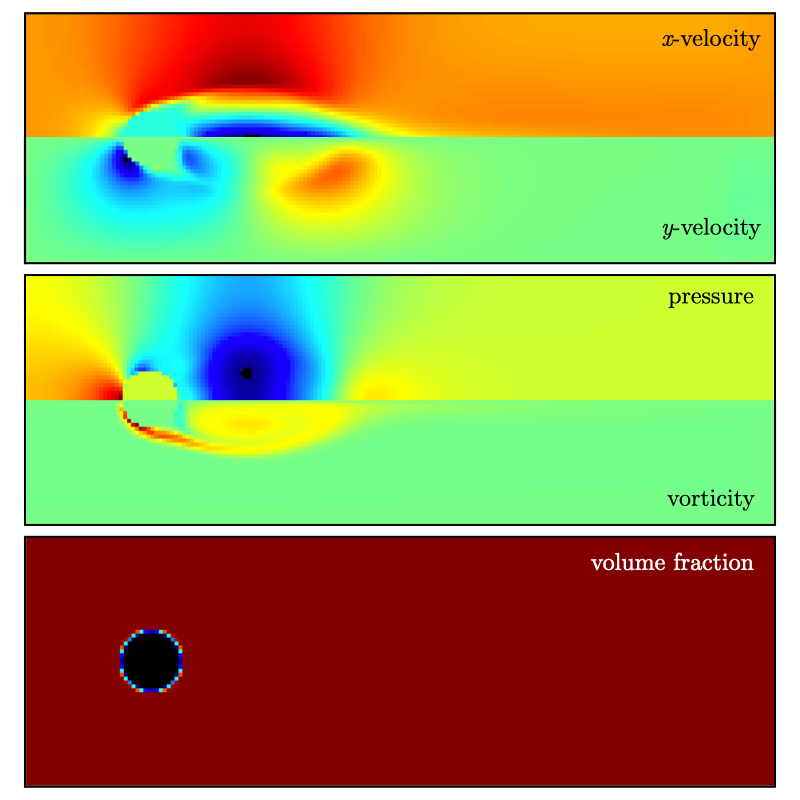
Fig. 15 : Contour plots of velocity components, vorticity, pressure and volume fraction at t = 25 ms on the coarse grid.
At this point, you have established a flow with a large recirculation zone in the wake of the cylinder, but the flow has not yet fully transitioned to periodic vortex shedding. The flow is depicted in Fig. 15 showing a few of the available contour plots at 25 ms. Note that the value of the fully covered cells is set to zero.
As can be seen from Fig. 15, the flow has not yet transitioned to the familiar Von-Karman alleys and two aspects of the current simulation can delay or even prevent the onset of vortex shedding:
the flow is initially symmetric and the transition to the familiar periodic flow is due to the growth of infinitesimal perturbations in the shear layer of the wake. Because the flow is artificially too symmetric, this transition can be delayed until round-off errors sufficiently accumulate.
the numerical dissipation introduced by this coarse grid results in an effective Reynolds number probably significantly lower than the value estimated above.
Before adding refinement levels, we will first pursue the simulation until the flow reaches a periodic vortex shedding state. To do so, restart the simulation from the checkpoint file generated at the end of the first run and set the final simulation time to 200 ms:
#-------------------------IO CONTROL----------------------------
...
amr.restart = chk_00437 # Restart from checkpoint ?
...
#----------------------TIME STEPING CONTROL----------------------
...
stop_time = 0.20 # final physical time
and restart the simulation
./PeleLMeX2d.gnu.MPI.ex input.2d-Re500 > logCoarseRun2.dat &
The flow has now fully transition and you can use Amrvis to visualize the series of vortex in the wake of the cylinder. In the next step, we will add finer grid patches around the EB geometry and in high vorticity regions.
Refinement of the computation
We will now add a first level of refinement. In the present simulation, the refinement criteria could be based on several characteristics of the flow: velocity gradients, vorticity, pressure, … In the following, we will simply use vorticity.
Additionally, by construction the geometry must be built to the finest level which act as a refinement criteria based on the gradient of volume fraction. This is beneficial in this case in order to help refine the cylinder boundary layer.
Start by increasing the number of AMR levels to one in the AMR CONTROL block:
amr.max_level = 1 # maximum level number allowed
Then provide a definition of the new refinement criteria in the REFINEMENT CONTROL block:
#--------------------REFINEMENT CONTROL------------------------
# Refinement according to the vorticity, no field_name needed
amr.refinement_indicators = VortL VortH
amr.VortL.max_level = 1
amr.VortL.value_less = -1000
amr.VortL.field_name = mag_vort
amr.VortH.max_level = 1
amr.VortH.value_greater = 1000
amr.VortH.field_name = mag_vort
The first line simply declares a set of refinement indicators which are subsequently defined. For each indicator, the user can provide a limit up to which AMR level this indicator will be used to refine. Then there are multiple possibilities to specify the actual criterion: value_greater, value_less, vorticity_greater or adjacent_difference_greater. In each case, the user specify a threshold value and the name of variable on which it applies (except for the vorticity_greater).
In the example above, the grid is refined up to level 1 at the location where the vorticity magnitude is above 1000 \(s^{-1}\) as well as on the cut cells by default (where the cylinder intersect with the edges of cell). Note that in the present case, the vorticity_greater was not used to ensure that regions of both low and high vorticity are refined.
With these new parameters, change the checkpoint file from which to restart and allow regridding upon restart by updating the following lines in the IO CONTROL block:
amr.restart = chk_03458 # Restart from checkpoint ?
, increase the stop_time to 300 ms in the TIME STEPING CONTROL block:
stop_time = 0.3 # final physical time
and start the simulation again (using multiple processor if available)
mpirun -n 4 ./PeleLMeX2d.gnu.MPI.ex input.2d-Re500 > log2Levels.dat &
Once again, use Amrvis to visualize the effects of refinement: after an initial transient, the flow return to a smooth periodic vortex shedding and the boundary layer of the cylinder is now significantly better captured but still far from fully refined. As a final step, we will add another level of refinement, only at the vicinity of the cylinder since the level 1 resolution appears sufficient to discretize the vortices in the wake. To do so, simply allow for another level of refinement:
amr.max_level = 2 # maximum level number allowed
and since the vorticity refinement criterion only refine up to level 1, the level 2 will only be located around the EB. Update the checkpoint file in the IO CONTROL block, increase the stop_time to 350 ms in the the TIME STEPING CONTROL and restart the simulation:
mpirun -n 4 ./PeleLMeX2d.gnu.MPI.ex input.2d-Re500 > log3Levels.dat &
You should obtain a flow with a vorticity field similar to Fig. 16. For the purpose of the present tutorial, this will be our final solution but one can see that the flow has not yet return to a periodic vortex shedding and additional resolution could be added locally to obtain smoother flow features.
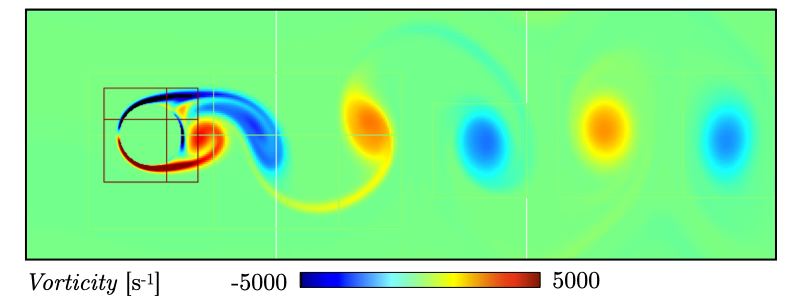
Fig. 16 : Contour plots of vorticity at t = 350 ms with 2 levels of refinements.