C10. Hagen–Poiseuille flow
Case description
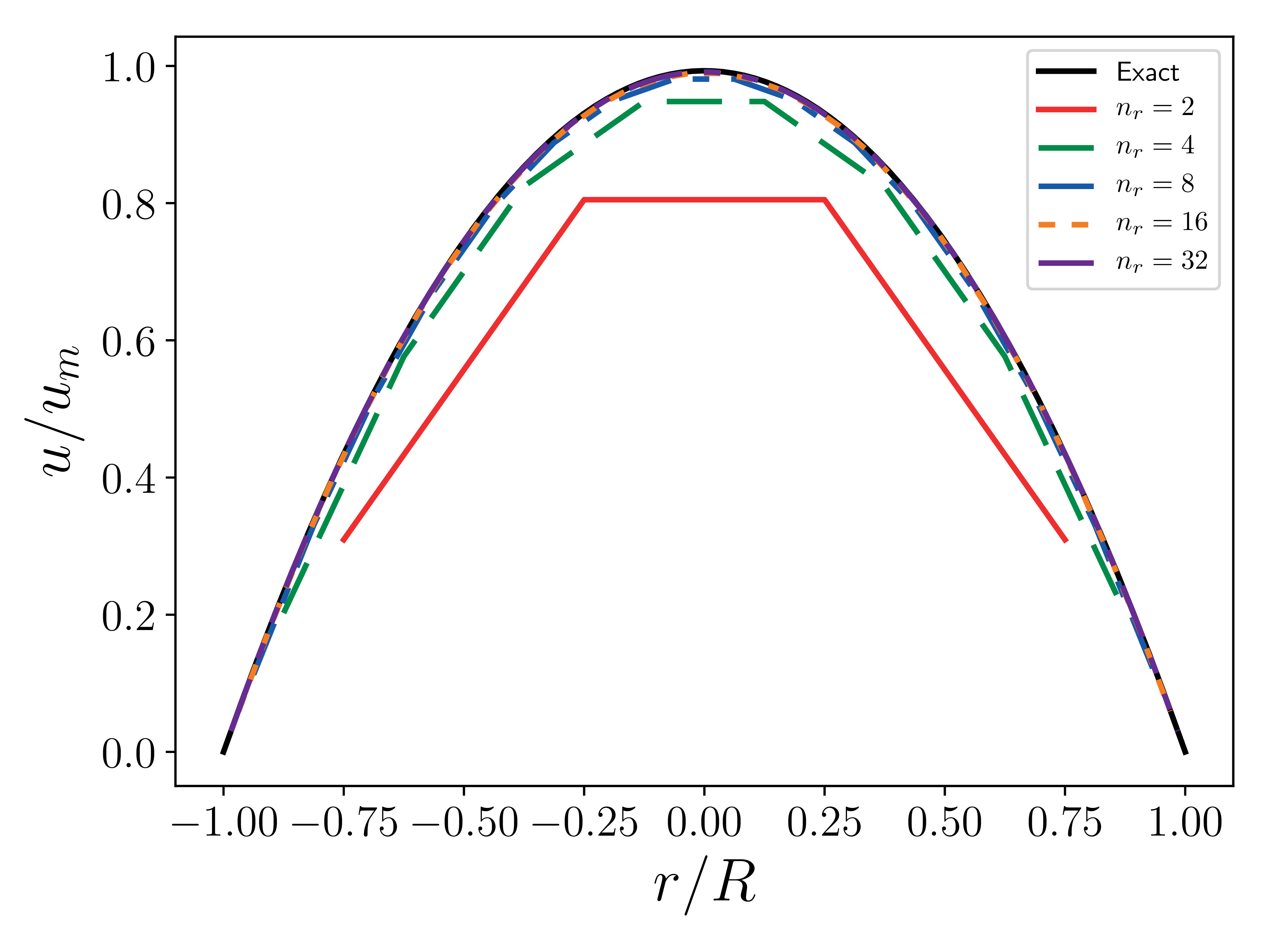
This is the standard Hagen–Poiseuille flow. The geometry is a \(x\)-direction aligned circular channel with imposed pressure boundary conditions at the inflow and the outflow to enforce a driving pressure gradient \(dp /dx\). For this case, the Mach number is set to 0.1, the Reynolds number to 100, and the Prandtl number to 0.71. The background pressure is atmospheric and the background temperature is 300K. The cylinder radius, \(R\), is 1cm and the cylinder length, \(L\), is 12cm. The simulations are performed for 5 flowthroughs, at which point in time quantities such as kinetic energy and momentum are converged.
The exact solution at steady state is
where \(G = -dp/dx\), and \(\mu\) is the dynamic viscosity.
Velocity profiles at \(x=6\) cm (channel center)
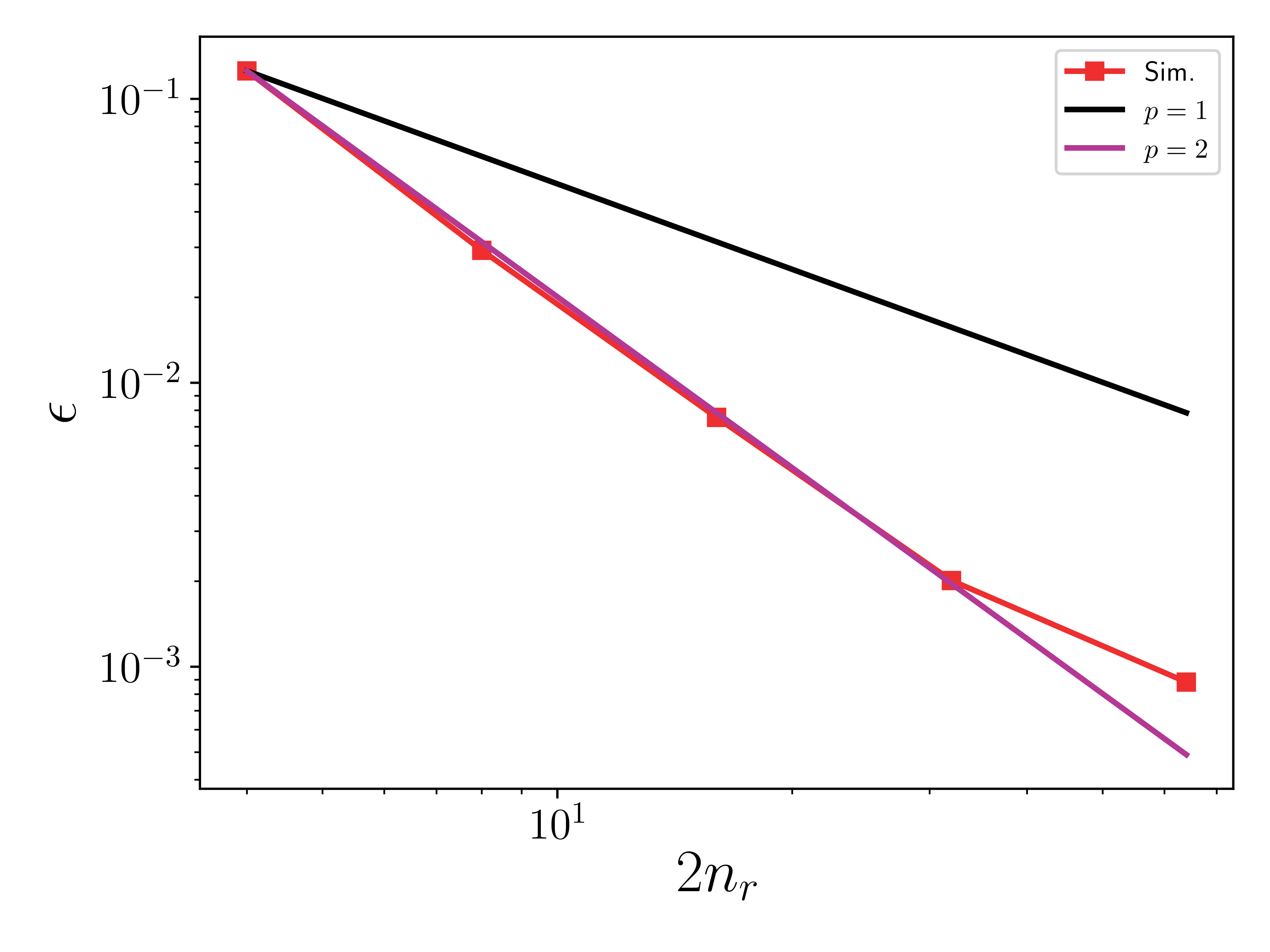
\(L_2\) error norm of velocity
The \(L_2\) error norm for a quantity \(s\) is defined as
where \(s^h\) is the numerical solution, \(s^*\) is the exact solution, and \(n_r\) is the number of cells per radius.
Note
The exact solution centerline velocity is adjusted by 0.7% to account for compressibility effects. The observance of second order behavior is attributed to the fact that this is a diffusion dominated problem and diffusion treatment at EB surfaces is second order.
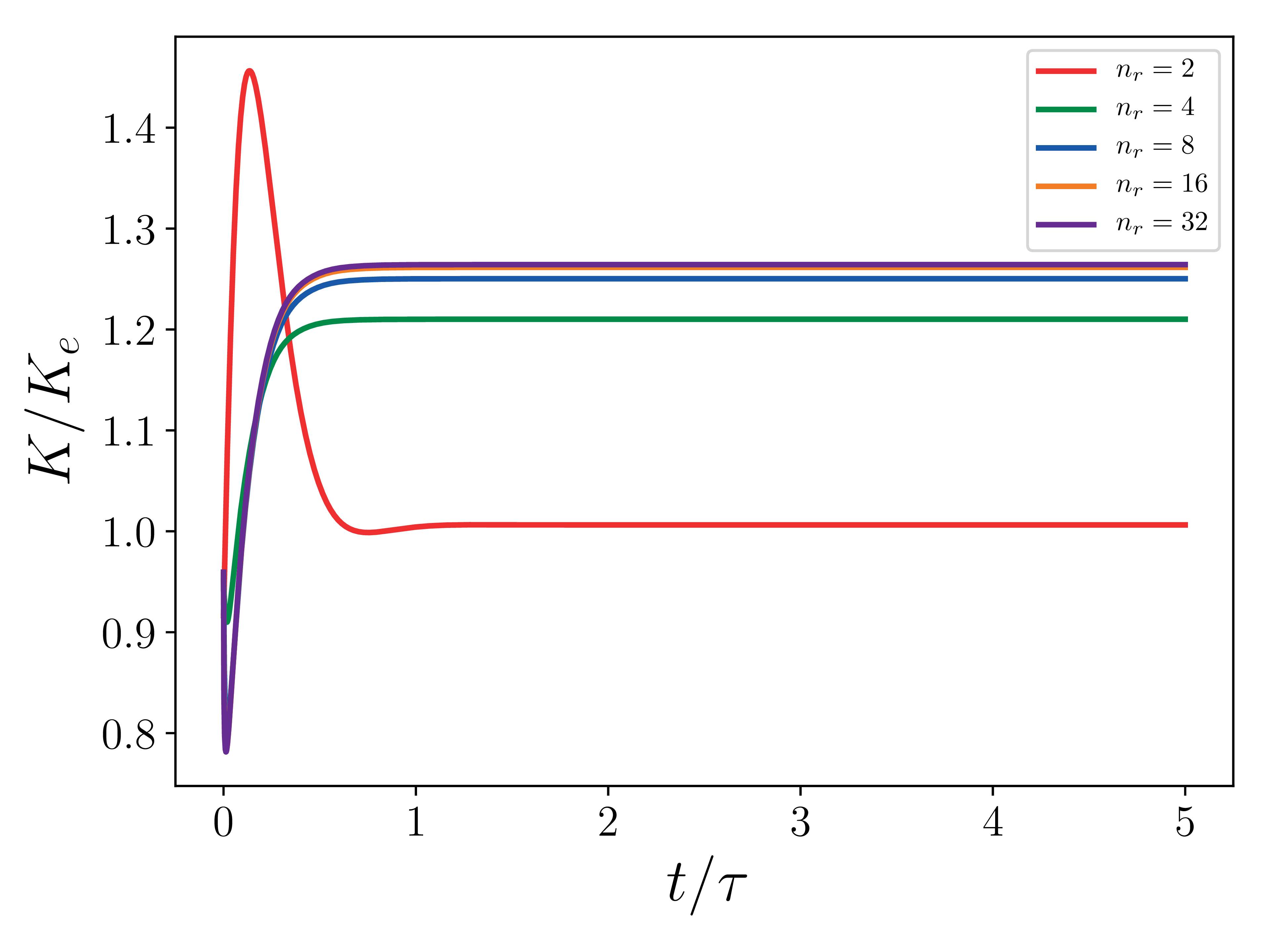
Time convergence of kinetic energy
Note
This figure shows that the compressible solution reached a steady state. It is not expected that the total integration of the kinetic energy in the domain match the incompressible value for integrated kinetic energy \(K_e\) because of compressibility effects.
Running study
paren=`pwd`
pelec="${paren}/PeleC3d.gnu.MPI.ex"
mpi_ranks=36
res=( 4 8 16 32 )
for i in "${res[@]}"
do
rm -rf "${i}"
mkdir "${i}"
cd "${i}" || exit
cp "${paren}/inputs_3d" .
ny="$((i*4))"
nx="$((i*4*3))"
srun -n ${mpi_ranks} "${pelec}" inputs_3d amr.n_cell="${nx} ${ny} ${ny}" > out
ls -1v *plt*/Header | tee movie.visit
cd "${paren}" || exit
done