C9. Acoustic wave in cylindrical channel
Case description
This is the case of an acoustic wave propagating in a cylindrical channel. The geometry is a \(x\)-direction aligned circular channel with periodic boundary conditions. The acoustic wave propagates along the \(x\) direction.
The density pulse at the center of the channel is defined as:
The background pressure is set to \(p_0 = 100000 erg/cm^3\), the background density is set to \(\rho_0 = 0.0014 g/cm^3\), \(\alpha=10^{-6} g/cm^3\), and \(\sigma=10cm\). The length of the channel is 100cm and the radius is 25cm. The simulations are performed for \(t=0.000625s\). The CFL is set to 0.001 to minimize time discretization errors.
Acoustic pulse at \(t=0.000625s\)
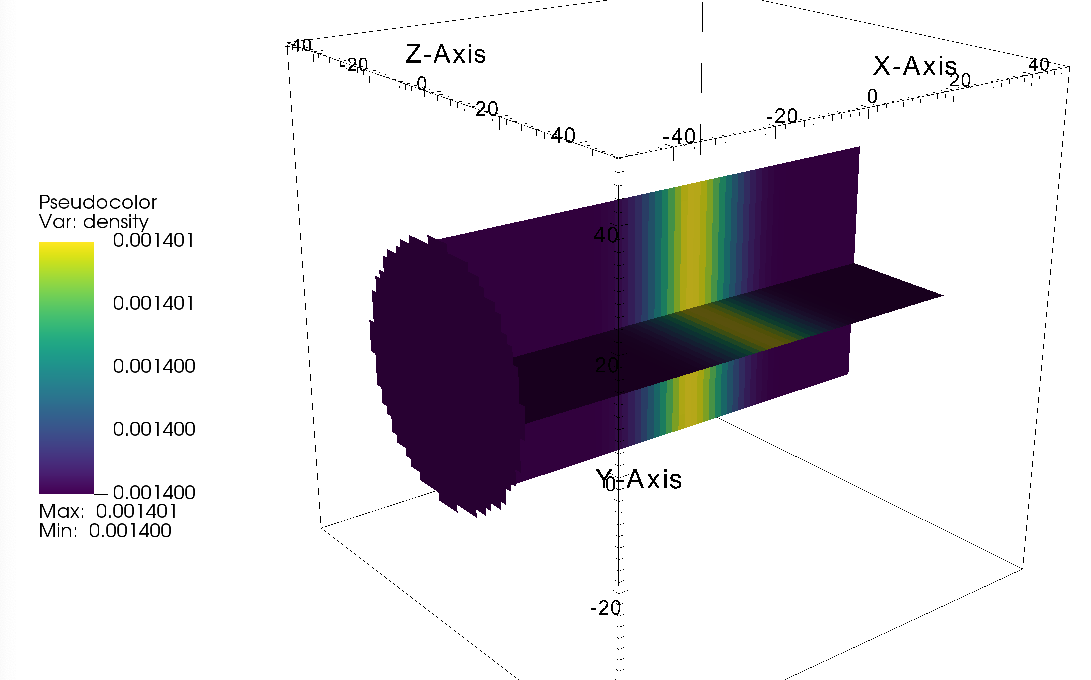
Density profiles in the centerline at \(t=0.000625s\)

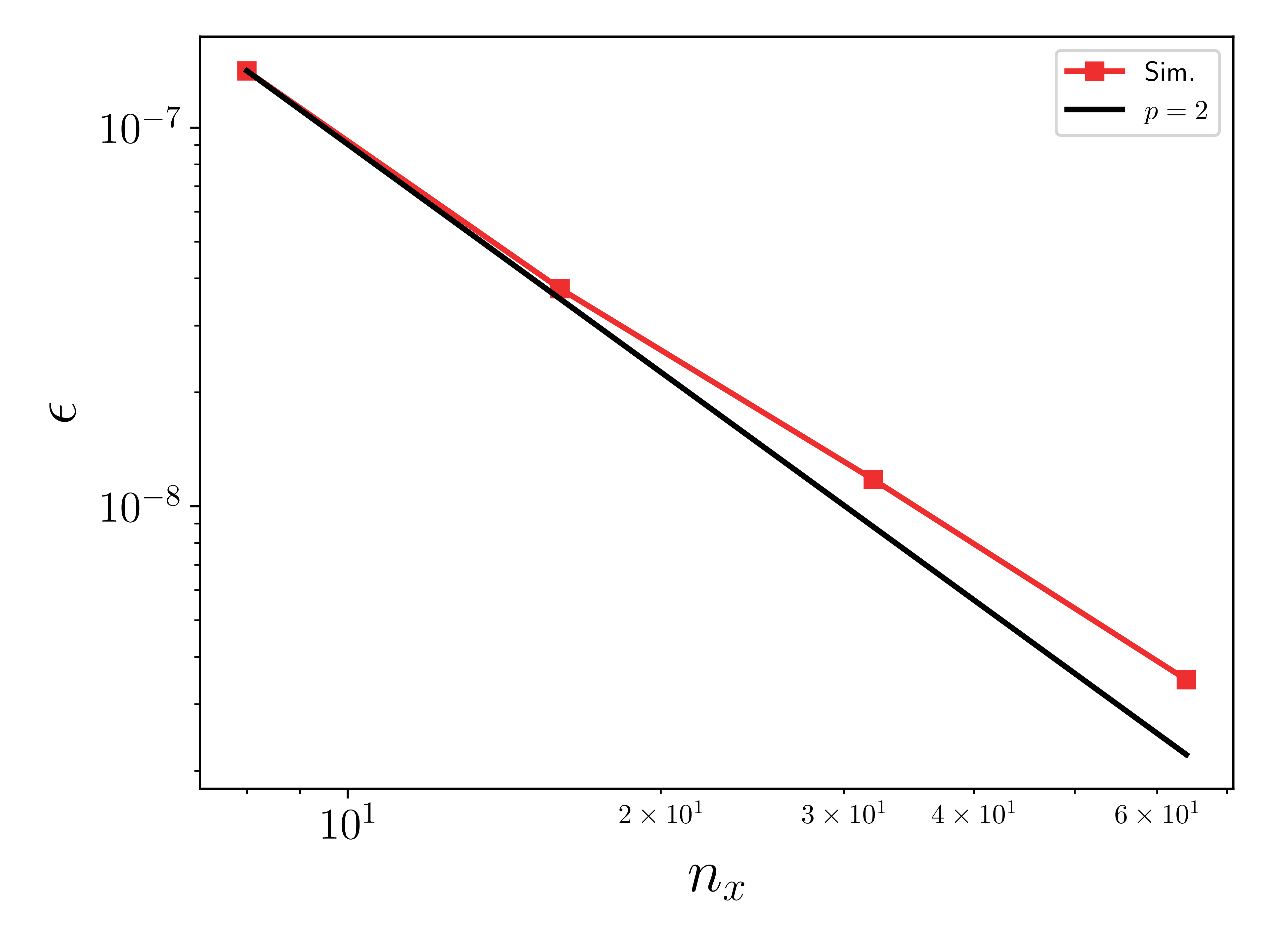
\(L_2\) error norm of density
The \(L_2\) error norm for a quantity \(s\) is defined as
where \(s^h\) is the numerical solution, \(s^*\) is the exact solution, and \(n_x\) is the number of cells in the \(x\)-direction.
Note
The second order convergence observed here is expected for this test case as all relevant physics happen in the direction perpendicular to the EB surface.
Running study
paren=`pwd`
pelec="${paren}/PeleC3d.gnu.MPI.ex"
mpi_ranks=36
res=( 8 16 32 64 )
for i in "${res[@]}"
do
rm -rf "${i}"
mkdir "${i}"
cd "${i}" || exit
cp "${paren}/inputs_3d" .
srun -n ${mpi_ranks} "${pelec}" inputs_3d amr.n_cell="${i} ${i} ${i}" > out
ls -1v *plt*/Header | tee movie.visit
cd "${paren}" || exit
done