C13. Supersonic vortex study
Case description
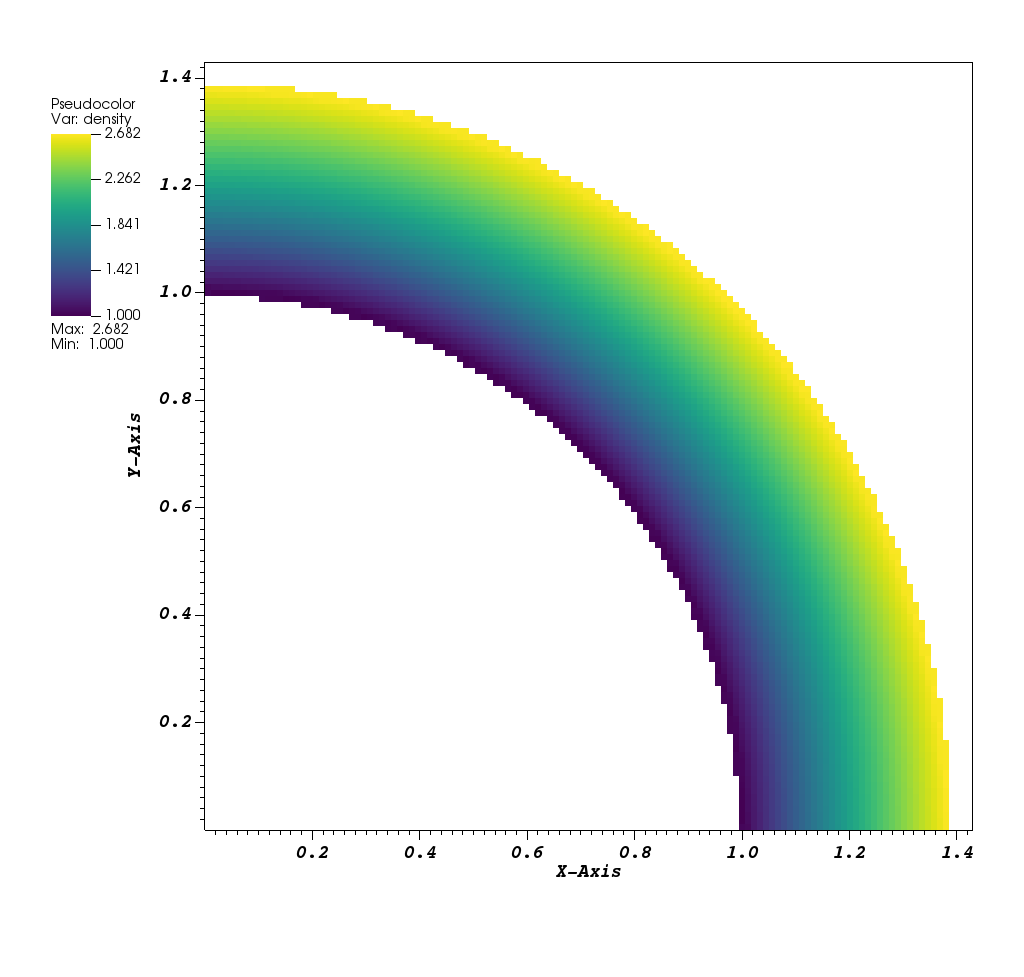
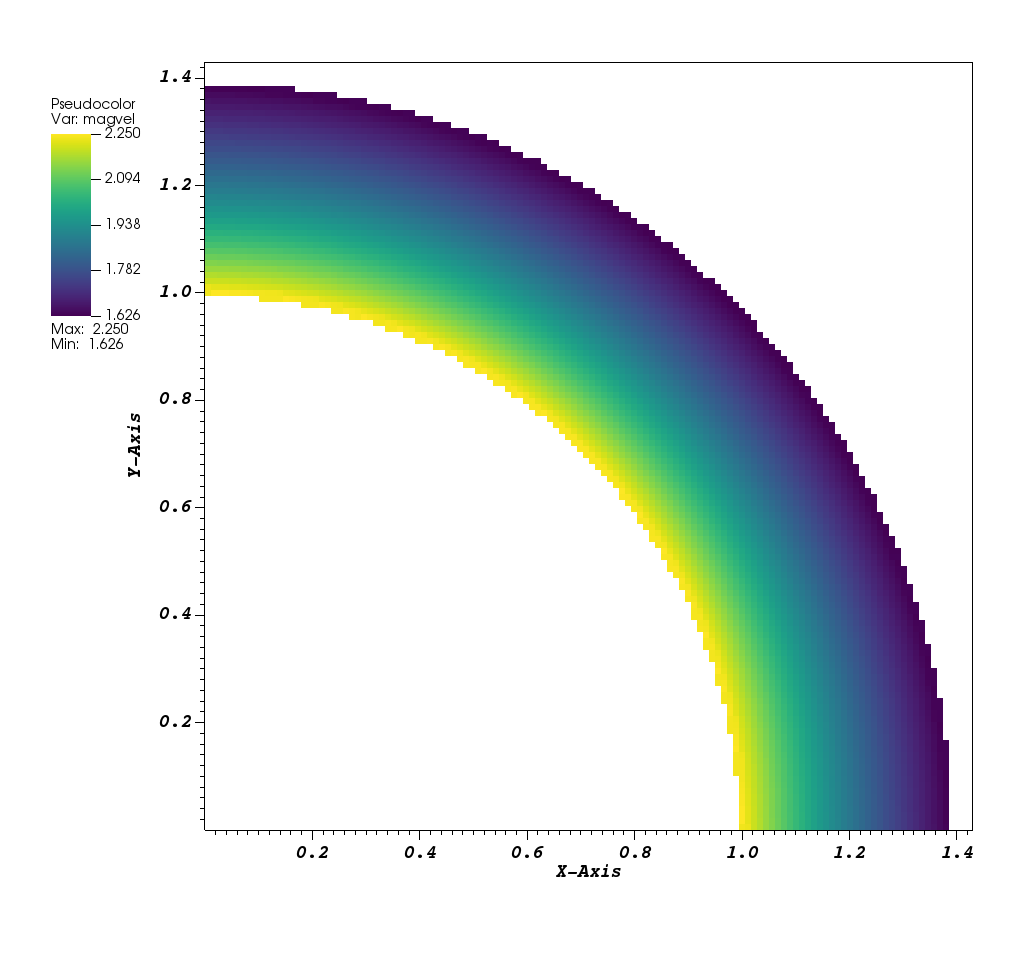
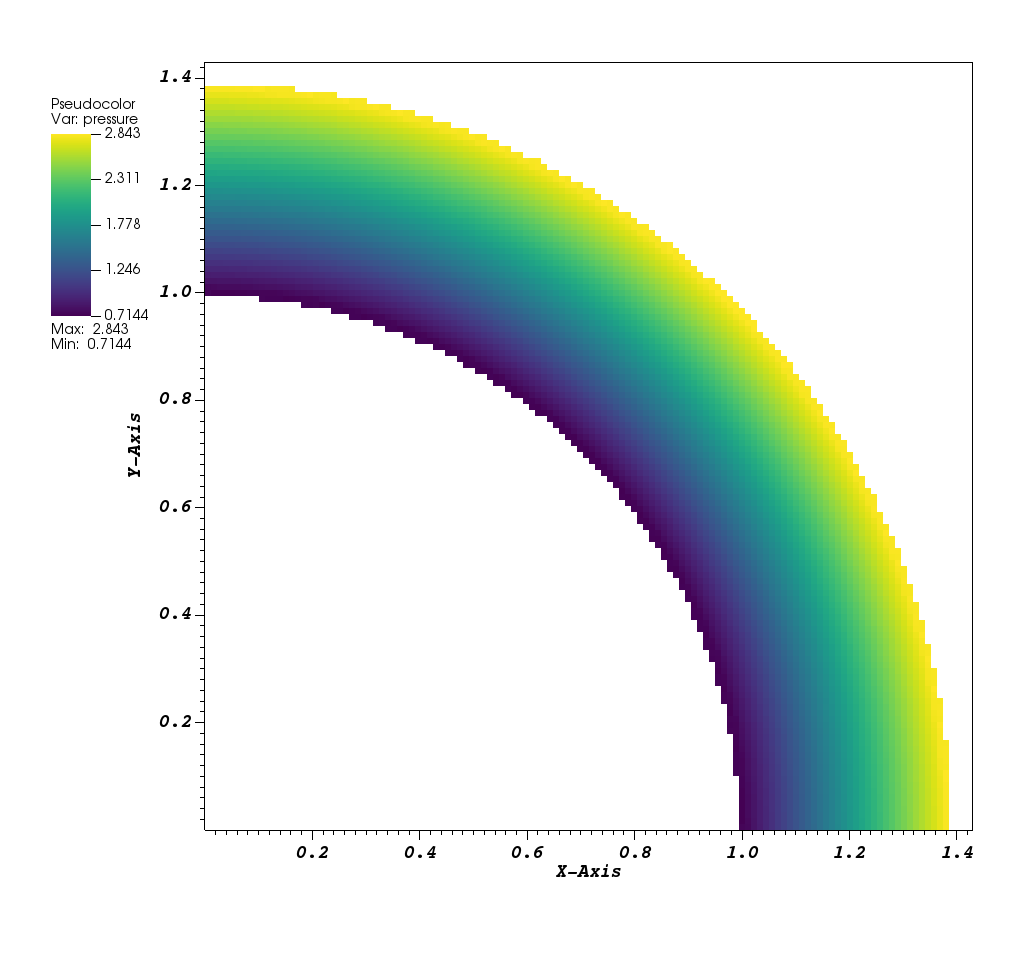
This is a supersonic flow around a quarter circle. It is described in Berger, Marsha, and Andrew Giuliani. “A state redistribution algorithm for finite volume schemes on cut cell meshes.” Journal of Computational Physics 428 (2021): 109820 and Aftosmis, Michael, Datta Gaitonde, and Theodore S. Tavares. “On the accuracy, stability, and monotonicity of various reconstruction algorithms for unstructured meshes.” (1994). It has an exact solution:
and \(u=a_i M_i cos(\theta)\), \(v=-a_i M_i cos(\theta``\), and \(p=\rho^\gamma/\gamma\). The inner radius, \(r_i=1.0\), the outer radius, \(r_o = 1.384\), the Mach number, \(M_i=2.25\), and the domain size \([0,0] \times [1.43,1.43]\). The initial solution is the exact solution and the exact solution is used at the boundaries conditions. The solution is marched for 10 flow throughs, until it reaches steady state.
Density
Magnitude of velocity
Pressure
Running study
paren=`pwd`
pelec="${paren}/PeleC3d.gnu.MPI.ex"
mpi_ranks=36
res=( 16 32 64 128 )
for i in "${res[@]}"
do
rm -rf "${i}"
mkdir "${i}"
cd "${i}" || exit
cp "${paren}/inputs_3d" .
hiz="$((0.3575*16/i))"
srun -n ${mpi_ranks} "${pelec}" inputs_3d amr.n_cell="${i} ${i} 4" geometry.prob_hi="1.43 1.43 ${hiz}" > out
ls -1v *plt*/Header | tee movie.visit
cd "${paren}" || exit
done