C12. Smooth periodic problem
Case description
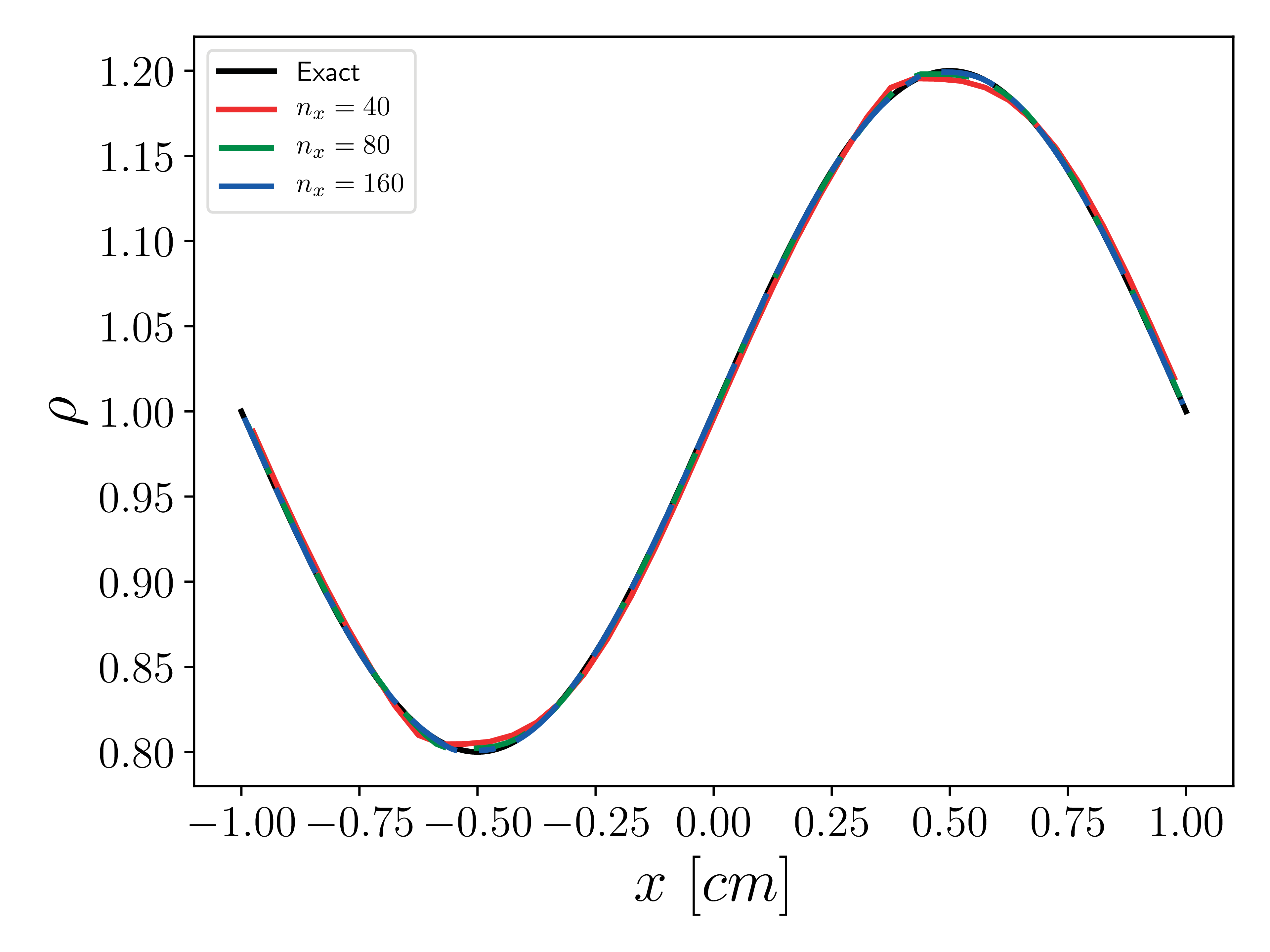
This is the standard smooth advection problem with \(u_0=1\), \(p_0=1\), and
This is an exact solution to the Euler equations and reduces them to simple linear advection with a constant velocity. Periodic boundary conditions are imposed. The gas constant is \(\gamma=1.4\). Usage of such a test case can be found in references such as Guan-Shan Jiang and Chi-Wang Shu. “Efficient implementation of weighted eno schemes”. J. Comp. Phys., 126:202–228 (1996) and Liska and Wendroff “Comparison of several difference schemes on 1D and 2D test problems for the Euler equations”. SIAM J. Sci. Comput., 25(3), 995–1017 (2006).
Simulations are performed in an \(x\)-direction aligned circular channel. The cylinder radius, \(R\), is 0.1cm and the cylinder length, \(L\), is 2cm. The simulations are performed until \(t=2\), at which point the wave is back at its starting location.
Density profiles in centerline
\(L_2\) error norm of density
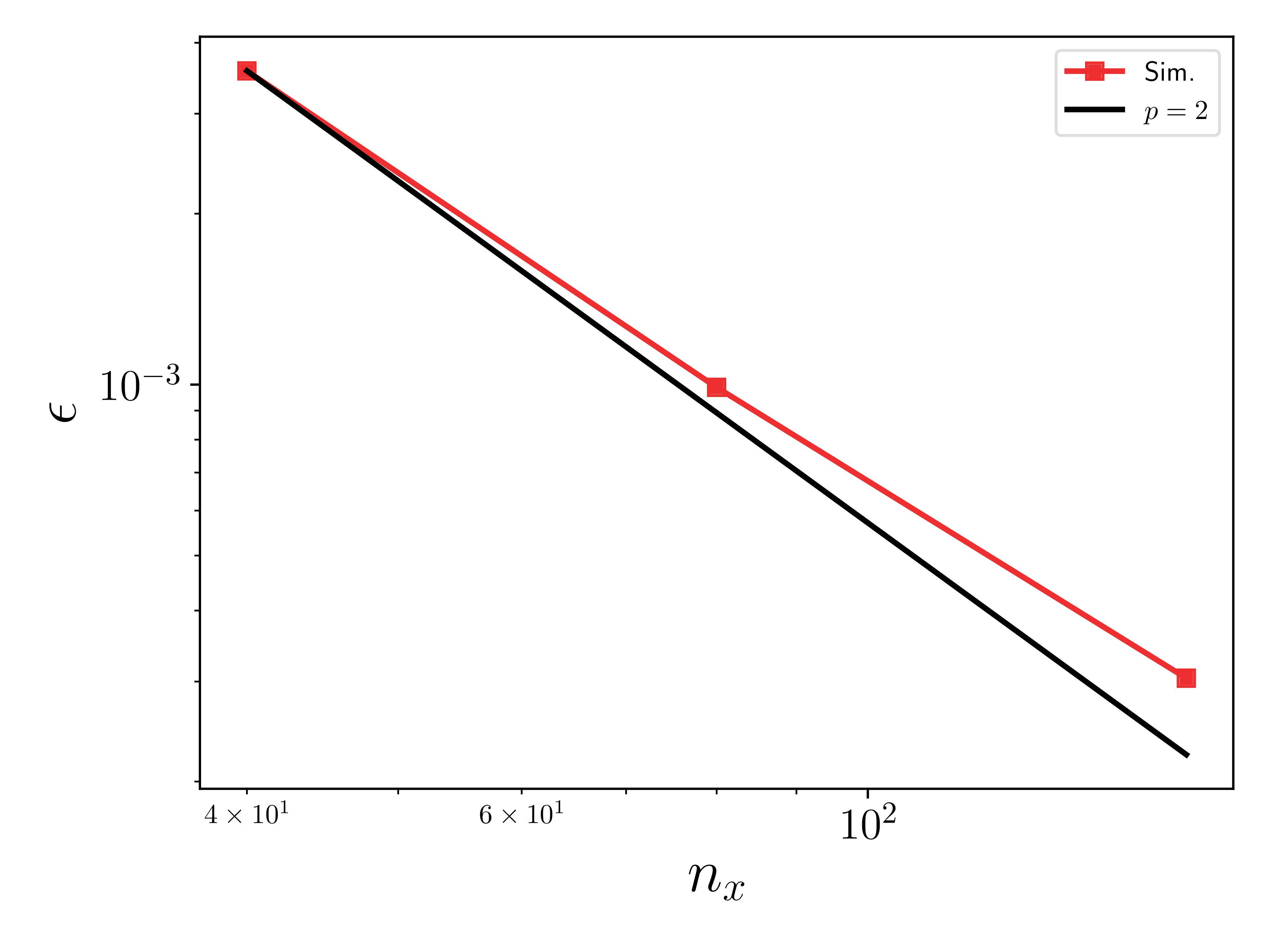
Note
The second order convergence observed here is expected for this test case as all relevant physics happen in the direction perpendicular to the EB surface.
Running study
paren=`pwd`
pelec="${paren}/PeleC3d.gnu.MPI.ex"
mpi_ranks=36
res=( 4 8 16 32 )
for i in "${res[@]}"
do
rm -rf "${i}"
mkdir "${i}"
cd "${i}" || exit
cp "${paren}/inputs_3d" .
ny="$((i*2))"
nx="$((i*10))"
srun -n ${mpi_ranks} "${pelec}" inputs_3d amr.n_cell="${nx} ${ny} ${ny}" pelec.fixed_dt=1e-5 > out
ls -1v ./*plt*/Header | tee movie.visit
cd "${paren}" || exit
done